示例Rc
下面以Rc类型为例,介绍其语义模型与实现.
Rc的语义模型
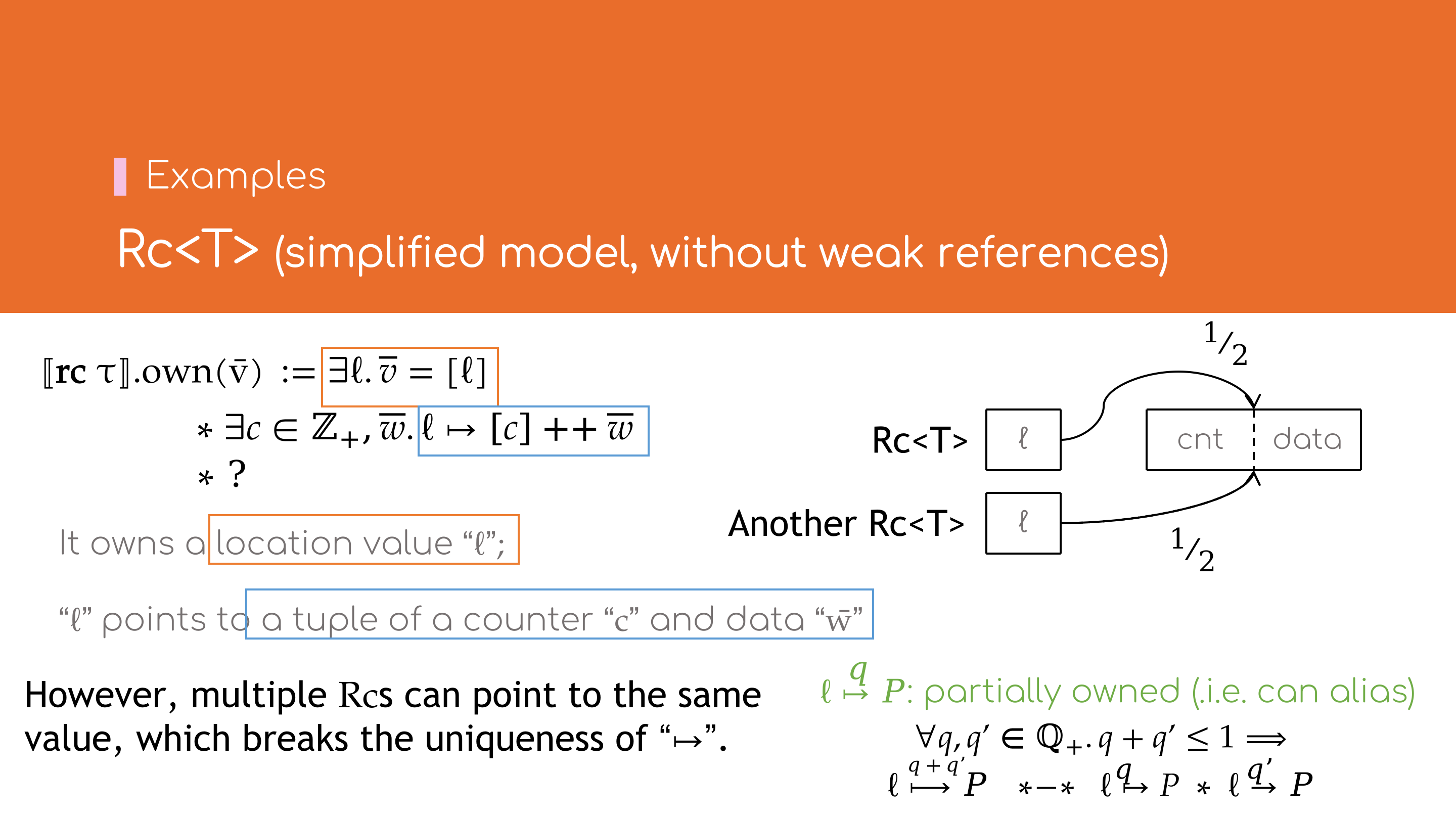
若不考虑弱引用,Rc的内存布局可以看作一个指针,指向一个含引用计数与承载数据的内存地址.
在\( \lambda_\text{Rust} \)中,引入\( \mathbf{rc} \, \tau \)类型以代表Rc<T>类型,若按以下方式定义
\[
\begin{array}{lll}
[\![ \mathbf{rc} \, \tau ]\!].\!\text{size}
& \mathrel{\mathop:}= 1 \\
[\![ \mathbf{rc} \, \tau ]\!].\!\text{own}(\bar{v})
& \mathrel{\mathop:}= \, \exists \ell. \bar{v} = [\ell]
& \bar{v} \text{是单个地址值} \ell \\
& \ast \, \exists c \in \mathbb{Z}_{+}, \bar{w}. \ell \mapsto c :: \bar{w}
& \ell \text{指向引用计数} c \text{与类型} \tau \text{的值} \bar{w} \\
& \ast \, ? & \text{应当如何表示共享所有权的值的约束?}
\end{array}
\]
(其中\(v :: l\)表示将值\(v\)插入列表\(l\)的首部而得的新列表),但这样的问题在于:
- \( \ell \mapsto c :: \bar{w} \)是独占所有权的,不能满足多个\( \mathbf{rc} \, \tau \)类型共享所有权的要求;
- 考虑到引用计数的存在,并不能简单地用\( [\![ \tau ]\!].\!\text{own}(\bar{w}) \)来\( \bar{w} \):
- 当\(c = 1\)时,\( \mathbf{rc} \, \tau \)表现为独占所有权,其语义与\( \mathbf{own} \, \tau \)类型一致;
- 当\(c > 1\)时,\( \mathbf{rc} \, \tau \)表现为共享所有权.
对于1,可以参考生存期token拆分,为\( \ell \mapsto P \)赋予有理数份额\(q\), 即\( \ell \overset{q}{\mapsto} P \)以表达部分所有权的语义.所有权拆分的方式如下 \[ \forall q, q' \in \mathbb{Q}_1, \ell, P. q + q' \le 1 \implies \ell \overset{q + q'}{\longmapsto} P \; \ast\!-\!\ast \; (\ell \overset{q}{\mapsto} P) \ast (\ell \overset{q'}{\mapsto} P) \]
\(\text{shared_own}\) Predict1

将\( \ell \mapsto c :: \bar{w} \)拆分为部分份额后,还须建立部分所有权份额\(q\)与引用计数\(c\)之间的约束.简单起见,引入 \[ \text{shared_own} \mathrel{\mathop:}= SemType \times Loc \times List(Val) \times \mathbb{N}_{+} \times \mathbb{Q}_1 \to iProp \] 再重新定义\( [\![ \mathbf{rc} \, \tau ]\!]\!.\!\text{own} \)如下 \[ \begin{array}{ll} [\![ \mathbf{rc} \, \tau ]\!]\!.\!\text{own}(\bar{v}) & \mathrel{\mathop:}= \, \exists \ell. \bar{v} = [\ell] \\ & \ast \, \exists c \in \mathbb{Z}_{+}, q \in \mathbb{Q}_1, \bar{w}. \ell \overset{q}{\mapsto} c :: \bar{w} \\ & \ast \, \text{shared_own}(\tau, \ell, \bar{w}, c, q) \end{array} \]
考察引用计数\(c\)与部分所有权份额\(q\)的关系:
- 当\(c = 1\)时,\(q = 1\),且\( \mathbf{rc} \, \tau \)的语义与\( \mathbf{own} \, \tau \)一致,有 \[ \forall \tau, \ell, \bar{w}. \text{shared_own}(\tau, \ell, \bar{w}, 1, 1) \; \ast\!-\!\ast \; [\![ \tau ]\!].\!\text{own}(\bar{w}) \ast \, \mathsf{Dealloc}(\ell, 1 + [\![ \tau ]\!].\!\text{size}) \]
- 当引用计数\(c\)加一时,同时可将份额为\(q + q'\)的部分所有权拆分为两个更小份额\(q\)与\(q'\)的部分所有权 \[ \begin{array}{l} \forall q, q' \in \mathbb{Q}_1, c, c' \in \mathbb{Z}_{+}, \tau, \ell, \bar{w}. q + q' \le 1 \implies \\ \quad \text{shared_own}(\tau, \ell, \bar{w}, c, q + q') \ast\!-\!\ast \\ \quad \text{shared_own}(\tau, \ell, \bar{w}, c + 1, q) \\ \quad \ast\, \text{shared_own}(\tau, \ell, \bar{w}, c + 1, q') \end{array} \]
- 当\(c > 1\)时,\( \mathbf{rc} \, \tau \)表现为共享所有权语义,该语义过于复杂,涉及Iris里面的高阶Ghost State的概念,此处暂不展开.
Rc的实现

下面以Rc类型中最常用的两个函数Rc::new与Rc::clone为例,介绍如何使用\( \lambda_\text{Rust} \)验证其正确性.
Rc::new的实现*

Rc::new简化后的逻辑如下
fn Rc::<T>::new(w: T) -> Rc<T> {
let x = Box::new(Cons(1, w));
x.into()
}
即先创建一个引用计数为1,值为w的Box,然后再将其转换为Rc(略去指针的实现细节,此处的类型转换可视为No-op).
求证: \[ \big\lbrace [\![ \tau ]\!].\!\text{own}(\bar{w}) \big\rbrace \; \mathbf{let} \, x = \text{Rc::new}(\bar{w}) \; \big\lbrace [\![ \mathbf{rc} \, \tau ]\!].\!\text{own}([x]) \big\rbrace \]
证明(概要):
展开\( \text{Rc::new} \)及\( [\![ \mathbf{rc} \, \tau ]\!].\!\text{own}([x]) \)得 \[ \begin{array}{lr} \big\lbrace [\![ \tau ]\!].\!\text{own}(\bar{w}) \big\rbrace \\ \quad \mathbf{let} \, x = \text{Box::new}(1 :: \bar{w}) \, ; & (1) \\ \quad \mathbf{let} \, x = x.\!\text{into}() & (2) \\ \left\lbrace \begin{array}{l} \exists c \in \mathbb{Z}_{+}, q \in \mathbb{Q}_1. \left( x \overset{q}{\mapsto} c :: \bar{w} \right) \ast \\ \text{shared_own}(\tau, x, \bar{w}, c, q) \end{array} \right\rbrace & (3) \end{array} \] 对(1)应用\( [\![ \mathbf{own} \, \tau ]\!].\!\text{own} \)的定义,有 \[ \begin{array}{lr} \big\lbrace [\![ \tau ]\!].\!\text{own}(\bar{w}) \big\rbrace \\ \quad \mathbf{let} \, x = \text{Box::new}(1 :: \bar{w}) \, ; \\ \left\lbrace \begin{array}{l} (x \mapsto 1 :: \bar{w}) \ast [\![ \tau ]\!].\!\text{own}(\bar{w}) \, \ast \\ \mathsf{Dealloc}(x, 1 + [\![ \tau ]\!].\!\text{size}) \end{array} \right\rbrace & (4) \end{array} \] 对(2), (4)式应用\( \text{shared_own} \)的第一个性质,得 \[ \begin{array}{lr} \left\lbrace \begin{array}{l} (x \mapsto 1 :: \bar{w}) \ast [\![ \tau ]\!].\!\text{own}(\bar{w}) \, \ast \\ \mathsf{Dealloc}(x, 1 + [\![ \tau ]\!].\!\text{size}) \end{array} \right\rbrace & (4) \\ \quad \mathbf{let} \, x = x.\!\text{into}() & (2) \\ \left\lbrace \begin{array}{l} \left( x \overset{1}{\mapsto} 1 :: \bar{w} \right) \ast \text{shared_own}(\tau, x, \bar{w}, 1, 1) \end{array} \right\rbrace & (5) \end{array} \] (5)式中令\(c = 1, q = 1\)得 \[ \begin{array}{lr} \left\lbrace \begin{array}{l} \exists q = 1, c = 1. \left( x \overset{q}{\mapsto} c :: \bar{w} \right) \ast \text{shared_own}(\tau, x, \bar{w}, c, q) \end{array} \right\rbrace & (5') \end{array} \] (3)得证.\(\square\)
Rc::clone的实现

Rc::clone简化后的逻辑如下
fn Rc::<T>::clone(x: &Rc<T>) -> Rc<T> { unsafe {
(*x).0 += 1;
let y = ptr::read(x);
y
} }
即首先将其引用计数自增1,然后再将x的指针浅复制一份得到y.
求证: \[ \big\lbrace [\![ \mathbf{rc} \, \tau ]\!].\!\text{own}([x]) \big\rbrace \; \mathbf{let} \, y = x.\!\text{clone}() \; \big\lbrace [\![ \mathbf{rc} \, \tau ]\!].\!\text{own}([x]) \ast [\![ \mathbf{rc} \, \tau ]\!].\!\text{own}([y]) \big\rbrace \]
证明(概要):
展开\( \text{Rc::clone} \),\( [\![ \mathbf{rc} \, \tau ]\!].\!\text{own}([x]) \) 及 \( [\![ \mathbf{rc} \, \tau ]\!].\!\text{own}([y]) \)得 \[ \begin{array}{lr} \left\lbrace \begin{array}{l} \exists c \in \mathbb{Z}_{+}, q \in \mathbb{Q}_1. \left( x \overset{q}{\mapsto} c :: \bar{w} \right) \ast \\ \text{shared_own}(\tau, x, \bar{w}, c, q) \end{array} \right\rbrace & (1) \\ \quad ({\mbox*}x).0 \, +\!= 1 \, ; & (2) \\ \quad \mathbf{let} \, y = \text{ptr::read}(x) & (3) \\ \left\lbrace \begin{array}{l} \exists c', c'' \in \mathbb{Z}_{+}, q', q'' \in \mathbb{Q}_1. \\ \left( x \overset{q'}{\mapsto} c' :: \bar{w} \right) \ast \text{shared_own}(\tau, x, \bar{w}, c', q') \; \ast \\ \left( y \overset{q''}{\mapsto} c'' :: \bar{w} \right) \ast \text{shared_own}(\tau, y, \bar{w}, c'', q'') \end{array} \right\rbrace & (4) \\ \end{array} \] 由(1), (2)式得 \[ \begin{array}{lr} \left\lbrace \begin{array}{l} \exists c \in \mathbb{Z}_{+}, q \in \mathbb{Q}_1. \left( x \overset{q}{\mapsto} c :: \bar{w} \right) \ast \\ \text{shared_own}(\tau, x, \bar{w}, c, q) \end{array} \right\rbrace & (1) \\ \quad ({\mbox*}x).0 \, +\!= 1 \, ; & (2) \\ \left\lbrace \begin{array}{l} \exists c \in \mathbb{Z}_{+}, q \in \mathbb{Q}_1. \left( x \overset{q}{\mapsto} (c + 1) :: \bar{w} \right) \ast \\ \text{shared_own}(\tau, x, \bar{w}, c, q) \end{array} \right\rbrace & (5) \\ \end{array} \] 现须证 \[ \begin{array}{lr} \left\lbrace \begin{array}{l} \exists c \in \mathbb{Z}_{+}, q \in \mathbb{Q}_1. \left( x \overset{q}{\mapsto} (c + 1) :: \bar{w} \right) \ast \\ \text{shared_own}(\tau, x, \bar{w}, c, q) \end{array} \right\rbrace & (5) \\ \quad \mathbf{let} \, y = \text{ptr::read}(x) & (3) \\ \left\lbrace \begin{array}{l} \exists c', c'' \in \mathbb{Z}_{+}, q', q'' \in \mathbb{Q}_1. \\ \left( x \overset{q'}{\mapsto} c' :: \bar{w} \right) \ast \text{shared_own}(\tau, x, \bar{w}, c', q') \; \ast \\ \left( y \overset{q''}{\mapsto} c'' :: \bar{w} \right) \ast \text{shared_own}(\tau, y, \bar{w}, c'', q'') \end{array} \right\rbrace & (4) \\ \end{array} \]

应用\( \text{shared_own} \)的第二个性质,将(5)式中的\( \text{shared_own}(\tau, x, \bar{w}, c, q) \)拆分为两个\( {}^q/{}_2 \)的份额 \[ \begin{array}{l} \text{shared_own}(\tau, x, \bar{w}, c, q) \; -\!\ast \\ \quad \text{shared_own}(\tau, x, \bar{w}, c + 1, {}^q/{}_2) \; \ast \\ \quad \text{shared_own}(\tau, x, \bar{w}, c + 1, {}^q/{}_2) \end{array} \] 再将\( x \overset{q}{\mapsto} (c + 1) :: \bar{w} \)也拆成两个\( {}^q/{}_2 \)的份额 \[ x \overset{q}{\mapsto} (c + 1) :: \bar{w} \; -\!\ast \; \left( x \overset{{}^q/{}_2}{\mapsto} (c + 1) :: \bar{w} \right) \ast \left( x \overset{{}^q/{}_2}{\mapsto} (c + 1) :: \bar{w} \right) \]

得 \[ \begin{array}{lr} \left\lbrace \begin{array}{l} \exists c \in \mathbb{Z}_{+}, q \in \mathbb{Q}_1. \\ \left( x \overset{{}^q/{}_2}{\mapsto} (c + 1) :: \bar{w} \right) \ast \left( x \overset{{}^q/{}_2}{\mapsto} (c + 1) :: \bar{w} \right) \ast \\ \text{shared_own}(\tau, x, \bar{w}, c + 1, {}^q/{}_2) \; \ast \\ \text{shared_own}(\tau, x, \bar{w}, c + 1, {}^q/{}_2) \end{array} \right\rbrace & (5') \end{array} \]

令\( q' = q'' = {}^q/{}_2 \),\(c' = c'' = c + 1\),则 \[ \begin{array}{lr} \left\lbrace \begin{array}{l} \exists c', c'' = c + 1, q', q'' = {}^q/{}_2. \\ \left( x \overset{q'}{\mapsto} c' :: \bar{w} \right) \ast \text{shared_own}(\tau, x, \bar{w}, c', q') \; \ast \\ \left( x \overset{q''}{\mapsto} c'' :: \bar{w} \right) \ast \text{shared_own}(\tau, x, \bar{w}, c'', q'') \end{array} \right\rbrace & (5'') \\ \quad \mathbf{let} \, y = \text{ptr::read}(x) & (3) \\ \left\lbrace \begin{array}{l} \exists c', c'' \in \mathbb{Z}_{+}, q', q'' \in \mathbb{Q}_1. \\ \left( x \overset{q'}{\mapsto} c' :: \bar{w} \right) \ast \text{shared_own}(\tau, x, \bar{w}, c', q') \; \ast \\ \left( y \overset{q''}{\mapsto} c'' :: \bar{w} \right) \ast \text{shared_own}(\tau, y, \bar{w}, c'', q'') \end{array} \right\rbrace & (4) \\ \end{array} \] (3)式中的\( \text{ptr::read} \)为浅复制,因此上式不难得证.\(\square\)